Some papers are famous and have gotten several citations. They always appear when I’m reading current papers. So I decided to write down the most critical parts (concerned mainly with myself, in another way) from these papers on this page.
Learning Deep Features for Discriminative Localization

This is a well-known work from CVPR2016, which has got 6.5k citation numbers up-to-date.
There are two parts that seem to be important to me: the comparison between global max pooling and global average pooling, as well as the framework.
GMP vs. GAP
We believe that GAP loss encourages the network to identify the extent of the object as compared to GMP which encourages it to identify just one discriminative part.
While GMP achieves similar classification performance as GAP, GAP outperforms GMP for localization.
GAP can focus on a wide range of pixels while GMP only depends on the most significant feature.
FRAMEWORK
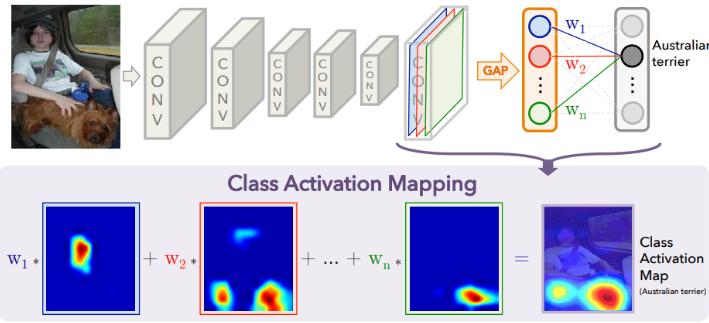
The output of the last convolutional layer is denoted as $f_k(x,y)$, while k means the channel. After GAP, which should be expressed as $F^k = \sum_{x,y}f_k(x,y)$, for a given class, the input to the softmax $S_c$, is $\Sigma_kw_k^cF_k$ where $w_k^c$ is weight corresponding to class c for unit k. $$ S_c = \sum_kw_k^c\sum_{x,y} f_k(x,y) = \sum_{x,y}\sum_k w_k^cf_k(x,y) $$ They did upsample in the middle of the framework to fit the size.
ABOUT weakly supervised: They meant weakly-supervised because the labels are image-level but localization is object-level
Learning to Compare: Relation Network for Few-Shot Learning

这篇文章的思路相当简单,而且比原型网络那篇更好理解,是最早的metric-base few-shot learning的一批,并且现在依然流行(其实现在的方法就是在这个基础上修改,大体的框架是一样的)。
FRAMEWORK
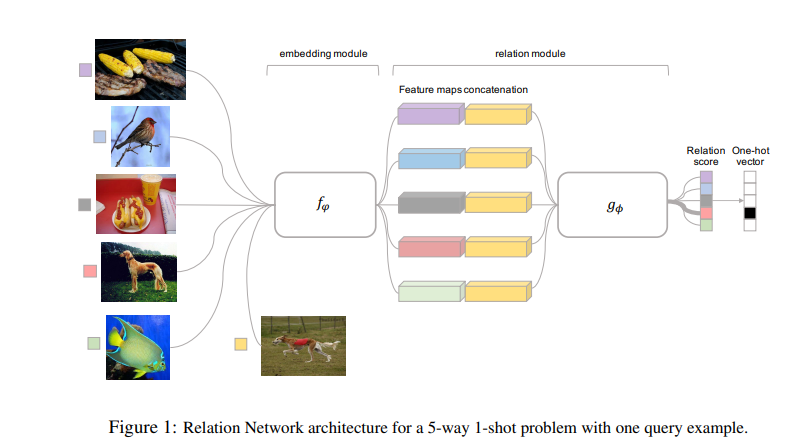
framework基本上一眼就能看明白,$f_\phi$和$g_\phi$都是卷积,池化,batch norm操作,没什么特别的。concatenation似乎就是从这里来的,现在基本也都是把query feature和support feature concatenate起来。其过程可用如下公式表示 $$ r_{i,j} = g_\phi(C(f_\phi(x_i),f_\phi(x_j))) $$ 其中$f_{\phi}$,$g_{\phi}$表示embedding module和relation module,函数$C(·,·)$表示concatenation。
ZERO-SHOT LEARNING
在zero-shot learning中,不再给support image,而是给semantic class embedding vector $v_c$,其过程可以用如下公式表示
$$
r_{i,j} = g_\phi(C(f_{\phi_1}(v_c),f_{\phi_2}(x_j)))
$$
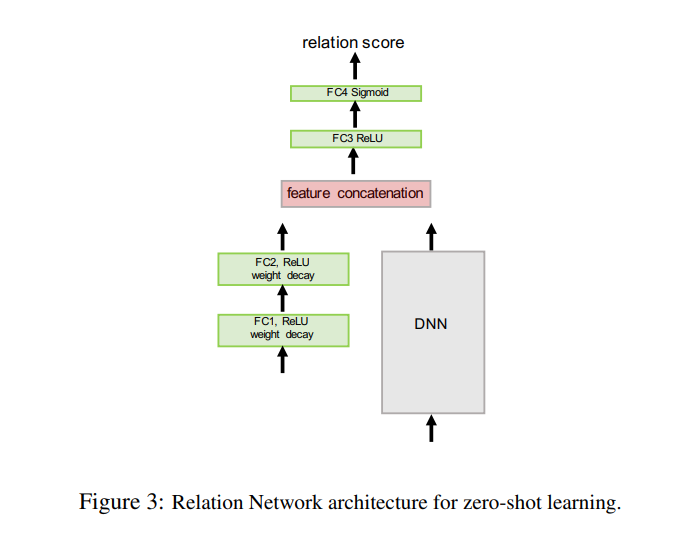
这里的DNN是训练好的模型,如VGG、Inception等。
和prototypical network的区别
Relation Network比原型网络的方法多了可学习的层,用来判别相似度度量,而在原型网络中是直接拿特定的相似度度量公式(如cosine similarity)